Black Friday was so last week, but the sales don't have to stop.
Hit up our online store to get 20% off every book from now until December 10th. But December 2nd, that's today, is the last day you can get FREE SHIPPING ON ANY ORDER OVER $50!
Black Friday was so last week, but the sales don't have to stop.
Hit up our online store to get 20% off every book from now until December 10th. But December 2nd, that's today, is the last day you can get FREE SHIPPING ON ANY ORDER OVER $50!
We've got some specials in the ol' online store today only.
You can get The Fightin' Scientists of Tesladyne and The Dogs of War for just $30 total (just pick the bundle option from either link)!
FOR BLACK FRIDAY ONLY, Mystery Shirts are marked down to just $10; Mugs are only $5; And Plush Robo Heads are a mere $20!
You'd be a fool not to take advantage of these deals. Oh, and shipping is free for orders over $50 between November 29th and December 2nd. Which, come to think of it, might be hard to pull off with all these discounts, but just throw hardcovers into your shopping cart until you make it! P.S. the hardcovers are on sale too! Just $20 each. Tesladyne Field Guides are down to $5. ULTRA Field Manuals are only $10.
It's pure insanity here. Don't be a wishy washy nerd with morals, take advantage of our disordered thinking and buy this stuff before we fix these prices!
Hello, everyone. Welcome to the fifth and final issue of Atomic Robo and the Dawn of a New Era. Hope you’re enjoying and also terrified for Alan. We can promise that it works out. I mean, everything does one way or another. Birthday parties work out. Extinction events work out.
That’s the Atomic Robo promise — you’ll get something between a birthday party and the end of life as we know it.
In fact, this week we can combine the fun of getting stuff and the existential dread of total doom because it’s New York Comiccon! This year you’ll find Scott Wegener at Table G-32 in Artists Alley next to our friends Chalk Please, Ain’t for Rent, Not Dunked Enough, Nights Errand, and Jimmy Wonderful.

What’s that? You can’t get yourself to NYCC? Well, have we got a deal for you. And the deal is you can save 10% off any purchase from our online store between Oct 2nd and 7th by using coupon code NYCC19 at checkout!
Everything is discounted from science nerd shirts to tabletop RPGs or hardcover collections or anything else! It can be yours for 10% off with NYCC19! Get to it!
Boy oh boy, we keep adding stuff to the online store. And we’re pretty excited about our latest addition. Check it!
This is only available for pre-order! It’s the perfect cloth armor to protect the meat avatar of a nerd in your life. Doubly so if that nerd is you.
And be sure to take advantage of Going Back to School Sale. Up to 30% off select items. Specifically these —
ULTRA Field Manual — This manual provides basic doctrinal discussion on the organization and operations of TFU and contains compartmentalized information essential to the security of physical constants, sustainability of life upon the Earth, and stability of the Solar System as well as Alternative Minkowski-Viable Spaces (AMVS) local to or intersecting with the Solar System.
Tesladyne Field Guide — This manual is for all employees, contractors, interns, staff, and innocent bystanders of Tesladyne.
Tesladyne Mug — Drink from the corporate chalice and be granted ETERNAL* LIFE!
*some conditions may apply
Dunno if you’ve seen our online store lately but there is a metric boatload of new items for you to check out.
First up did you know you can get the official Atomic Robo RPG with the Majestic 12 supplement at an absurdly deep discount price? Both of these books are out of print and supplies are limited. Get them before they’re all gone!
We’ve got the Tesladyne Labs patch. It’s cute. You sew it onto things.
There’s also the ULTRA patch. It’s menacing. It sews itself onto things and you don’t ask why.
You want stickers? How about two of them — The Evolution of Robo and Our Friend the Atomic Robot.
And of course there’s the hardcover edition of Atomic Robo and the Spectre of Tomorrow.
We got some new goodies in ye olde onlinee storee.
First up there’s the Spectre of Tomorrow print set featuring the cover for the trade paperback, the hardcover, and every issue including our infamous and bizarre toilet issue.
Next up there’s the Sticker Pack featuring a She-Devil, a Doctor Dinosaur, a Sparrow, and a dead Robo because...? Don't question it.
And, lastly, there is no better way to present your security credentials than to hang them from your very own officially licensed Tesladyne Lanyard.
And, hey, why not pick up a book or twelve while you’re at it?
You know the drill, folks!
We’ll be at ALA this weekend. You can catch Scotty McWegener there all day every day like the marathoner he is, but Brian O’Clevy will be there from noon to close on Saturday and all day Sunday.
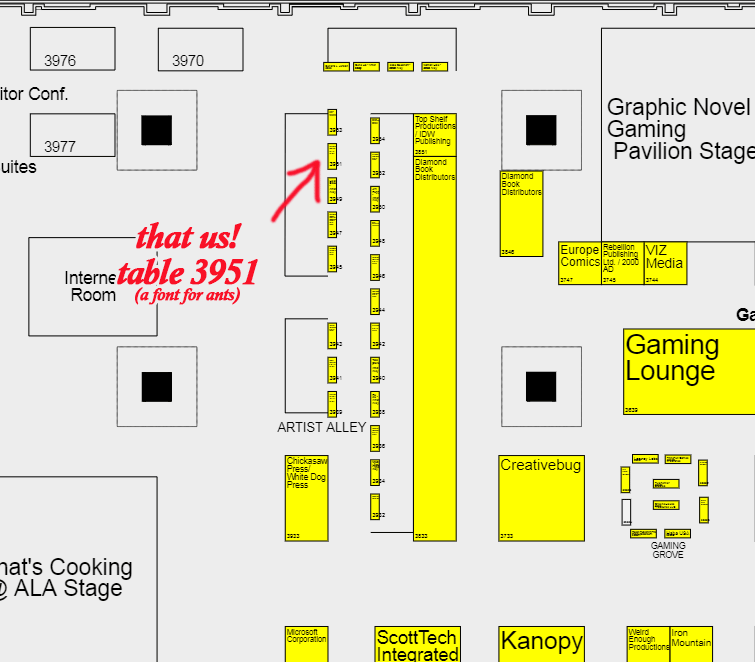
Swing by Table 3951 in Ye Olde Artiste Alleye. If you find the big IDW booth, we’re right behind ‘em! We’ll have hardcovers, Tesladyne branded school supplies, prints, and more!
Our online store is back and you can check it out right now clicky click click! Our new warehouse and new storefront provided by the fine folks at DFTBA offers more and better shipping options including less expensive shipping for you international customers! Give it a look and celebrate the new store with coupon code TESLALAUNCH19 to get 10% off your purchase.
Meanwhile we’ll be at ALA in Washington DC June 20 - 25th. You can find us at Table 3951. MAP —
Howdy, folks!
Just a little bampity bomp bump for our latest Kickstarter campaign to bring The Nicodemus Job to hardcover and to print Doctor Dinosaur’s idiotic time travel tourism guide that you definitely should not read.
We hit our funding goal and now it’s just a matter of knocking out some more Stretch Goals to deliver the fanciest rewards possible! The campaign ends around midnight tonight, so toss some money into the pile before it’s too late!
You folks ready for a new Kickstarter? TOO BAD HERE IT IS!
We’re making a fancy hardcover edition of our newest book, Real Science Adventures: The Nicodemus Job. This stunning collection was drawn by Meredith McClaren, colored by J.N. Wiedle (Chapter One) and Shan Murphy (Chapters Two through Five), lettered by Tess Stone, edited by Lee Black, written by Brian Clevinger, with layout/design by Eric Trautmann.
Oh and uh also Doctor Dinosaur wrote a book and we’re contractually obligated to help him promote it. But our promotion doesn’t have to be polite. So, it’s called Doctor Dinosaur’s Time Travel Through the Back Door, and it’s terrible. Just, seriously, a big stupid mess of a book.
We’ve got all kinds of goodies like digital rewards, prints, more pages in both books, and original art. Hope you check it out!